Solve the Sudoku
Problem Statement - link #
Given an incomplete Sudoku configuration in terms of a 9 x 9 2-D square matrix (grid[][]), the task to find a solved Sudoku. For simplicity, you may assume that there will be only one unique solution.
Your Task:
You need to complete the two functions:
SolveSudoku(): Takes a grid as its argument and returns true if a solution is possible and false if it is not.
printGrid(): Takes a grid as its argument and prints the 81 numbers of the solved Sudoku in a single line with space separation.
NOTE: Do not give a new line character after printing the grid. It has already been taken care of in the Driver Code.
Expected Time Complexity: O(9^(N*N))
Expected Auxiliary Space: O(N*N)
Examples #
Sample Sudoku for you to get the logic for its solution:
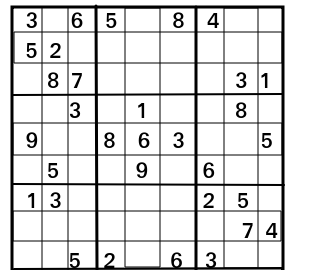
Example 1:
Input:
grid[][] =
[[3 0 6 5 0 8 4 0 0],
[5 2 0 0 0 0 0 0 0],
[0 8 7 0 0 0 0 3 1 ],
[0 0 3 0 1 0 0 8 0],
[9 0 0 8 6 3 0 0 5],
[0 5 0 0 9 0 6 0 0],
[1 3 0 0 0 0 2 5 0],
[0 0 0 0 0 0 0 7 4],
[0 0 5 2 0 6 3 0 0]]
Output:
3 1 6 5 7 8 4 9 2
5 2 9 1 3 4 7 6 8
4 8 7 6 2 9 5 3 1
2 6 3 4 1 5 9 8 7
9 7 4 8 6 3 1 2 5
8 5 1 7 9 2 6 4 3
1 3 8 9 4 7 2 5 6
6 9 2 3 5 1 8 7 4
7 4 5 2 8 6 3 1 9
Constraints #
0 ≤ grid[i][j] ≤ 9
Solutions #
class Solution {
public:
bool isSafe(int grid[N][N], int r, int c, int n){
for(int i=0;i<N;i++)
if(grid[i][c]==n || grid[r][i]==n)
return false;
int sq = sqrt(N);
int sr = r - r%sq;
int sc = c - c%sq;
for(int i=sr;i<sr+sq;i++)
for(int j=sc;j<sc+sq;j++)
if(grid[i][j]==n)
return false;
return true;
}
//Function to find a solved Sudoku.
bool SolveSudoku(int grid[N][N])
{
// Your code here
int i,j,yes=0;
for(i=0;i<N;i++){
for(j=0;j<N;j++)
if(grid[i][j]==0){
yes = 1;
break;
}
if(yes) break;
}
if(!yes) return true;
for(int n=1;n<10;n++){
if(isSafe(grid,i,j,n)){
grid[i][j]=n;
if(SolveSudoku(grid)) return true;
grid[i][j]=0;
}
}
return false;
}
//Function to print grids of the Sudoku.
void printGrid (int grid[N][N])
{
// Your code here
for(int i=0;i<N;i++){
for(int j=0;j<N;j++)
cout << grid[i][j] << " ";
// cout<<endl;
}
}
};