Construct Binary Search Tree from Preorder Traversal
Problem Statement - link #
Given an array of integers preorder, which represents the** preorder traversal** of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right
Examples #
Example 1:
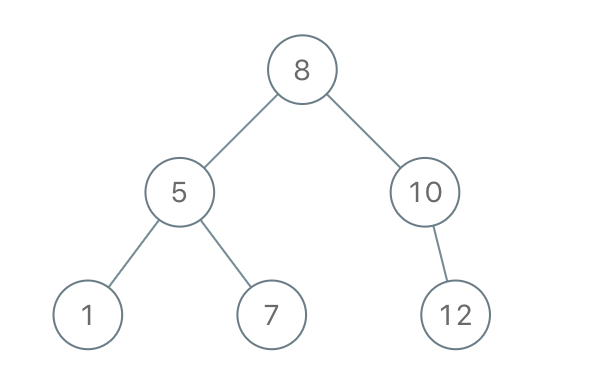
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
Example 2:
Input: preorder = [1,3]
Output: [1,null,3]
Constraints #
1 <= preorder.length <= 1001 <= preorder[i] <= 10^8- All the values of preorder are unique.
Solutions #
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void recurse(TreeNode* root, int val){
if(root->val > val)
if(root->left == NULL)
root->left = new TreeNode(val);
else
recurse(root->left,val);
else
if(root->right == NULL)
root->right = new TreeNode(val);
else
recurse(root->right,val);
}
TreeNode* bstFromPreorder(vector<int>& preorder) {
TreeNode* root = new TreeNode(preorder[0]);
for(int i=1; i<preorder.size(); i++)
recurse(root,preorder[i]);
return root;
}
};